Evaluate the Integral by Changing to Polar Coordinates

SE 4x - y da where R is the region in the first quadrant enclosed by the circle x2 y2 - 16 and the lines 0 and y x 52 - 12 3 V2. Calculus questions and answers.

Solved Evaluate The Given Integral By Changing To Chegg Com

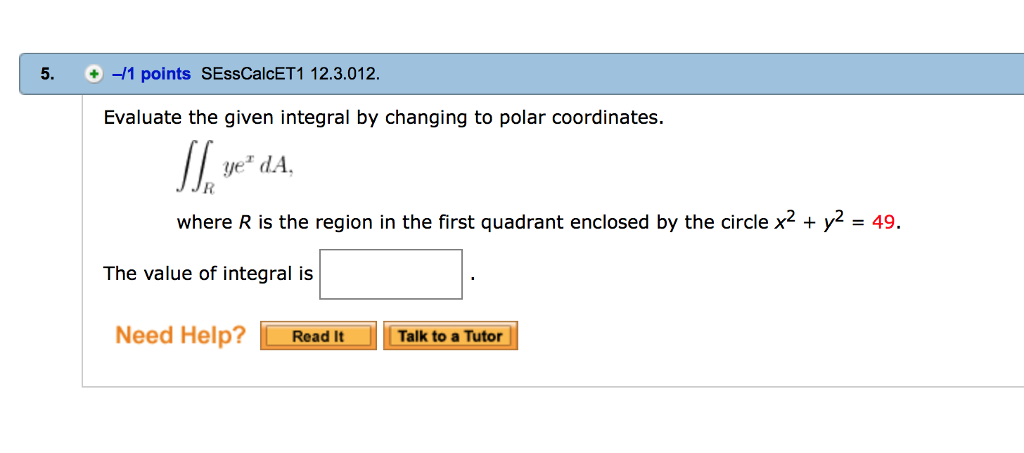
R ye x dA where R is the region in the first quadrant enclosed by the circle x 2 y 2 25.

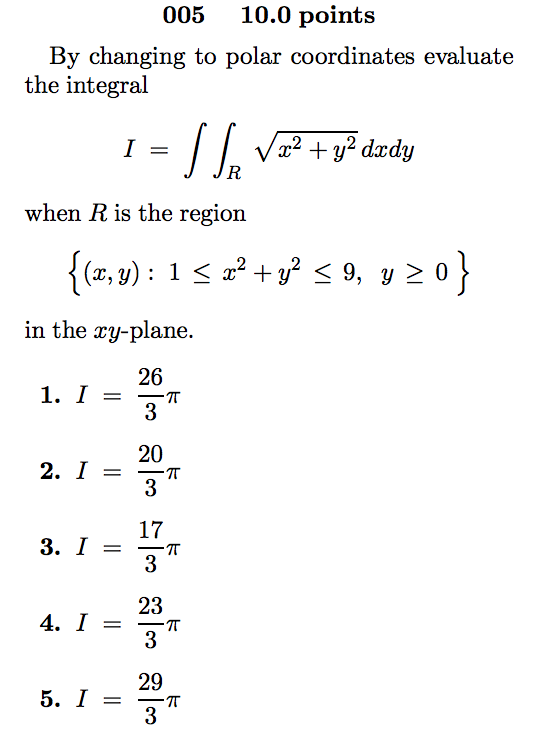
. Evaluate the given integral by changing to polar coordinates. Find step-by-step Calculus solutions and your answer to the following textbook question. Haidenfirkins7160 is waiting for your help.

Get the free Polar Integral Calculator widget for your website blog Wordpress Blogger or iGoogle. So then x2 y2 r2. Evaluate the given integral by changing to polar coordinates.

Find more Mathematics widgets in WolframAlpha. So the integral becomes Z Z D x2 y211 2 dxdy Z 2ˇ 0 Z 2 0 r211 2 rdrd. 0 2 0 2 x x 2 x y d y d x.

R 4x y dA where R is the region in the first quadrant enclosed by the circle x2 y2 16 and the lines x 0 and y x. θ after putting in above expressiona nd corresponding to that changing the limiting value. Add your answer and earn points.

Add answer 5 pts. Evaluate the given integral by changing to polar coordinates. One of the reasons we want to be able to integrate in polar coordinates is that some integrals work out nicely in one coordinate system and are ugly in another.

Double integral of 4x y dA where R is the region in the first quadrant enclosed by the circle x2 y2 4 and the lines x 0 and y x. Sin x2 y2 dA R where R is the region in the first quadrant between the circles with center the origin and radii 2 and 3. Evaluate the given integral by changing to polar coordinates.

By changing to polar coordinates evaluate the integral integralintegral_D x2 y252 dxdy where D is the disk x2 y2 le 36. Evaluate the given integral by changing to polar coordinates. Expression will change into.

Sinx2 y2 dA R where R is the region in the first quadrant between the circles with center the origin and radii 1. Sinx2 y2 dAR where R is the region in the first quadrant between the circles with center the origin and radii 3 and 4 1 See answer. Evaluate the given integral by changing to polar coordinates.

Set up the graph and evaluate the proper function of variable formula in the polar to evaluate using polar coordinates are the layout of. Integrating the given equation after converting to polar coordinates. 532 Evaluate a double integral in polar coordinates by using an iterated integral.

Where D is the region in the first quadrant that lies between the circles x2 y2. The double integrals evaluate integral can be evaluated by changing polar. Now since Dis a disk of radius 2 we have 0 r 2 and 0 2ˇ.

Sin x2 y2 dA R where R is the region in the first quadrant between the circles with center the origin and radii 3 and 5. Ex2 y2 dA D where D is the region bounded by the semicircle x 16 y2 and the yaxis Videos Step-by-step answer. Find polar coordinates is outlined in cases to find polar coordinates drill down into cartesian coordinates to evaluate integral by changing to polar double coordinates to evaluate.

Evaluate the given integral by changing to polar coordinates. Evaluate the integral by changing to polar coordinates. By changing to polar coordinates evaluate the integral RR D x2y211 2 dxdy where Dis the disk x 2 y 4.

Use the given transformation to evaluate the. Sin x2 y2 dA R where R is the region in the first quadrant between the circles with center the origin and radii 3 and 5. Evaluate the given integral by changing to polar coordinates.

533 Recognize the format of a double integral over a general polar region. Evaluate the given integral by changing to polar coordinates. θ and y r sin.

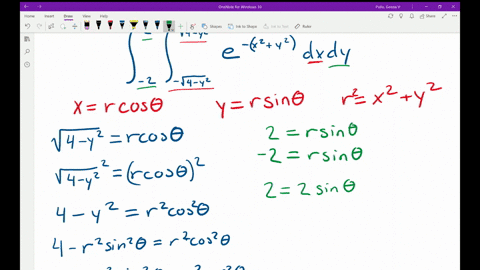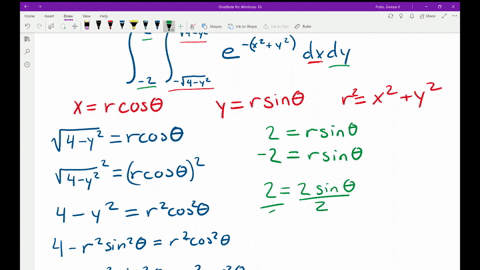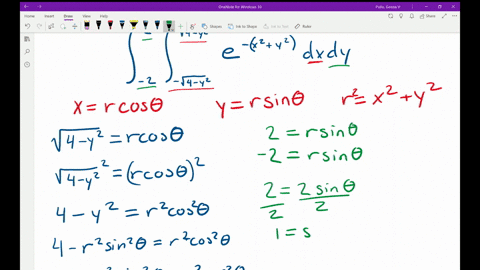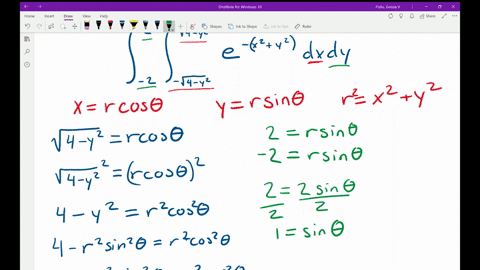
To change the function and limits of integration from rectangular coordinates to polar coordinates well use the conversion formulas xrcostheta yrsintheta and r2x2y2. Remember also that when you convert dA or dy dx to polar. Evaluate the given integral by changing to polar coordinates.

Double integral exp-x2-y2 da where D is the region bounded by the semicircle x4-y212 and the y-axis. Let is assume x r cos. Evaluate the given integral by changing to polar coordinates.

531 Recognize the format of a double integral over a polar rectangular region. Ff sin x² y² dA where Ris the region in the first quadrant between the circles with center the origin and radii 1 and 3. 534 Use double integrals in polar coordinates to calculate areas and volumes.

To switch to polar coordinates we let x rcos and y rsin. In polar coordinates dxdy rdrd. Evaluate the given integral by changing to polar coordinates.

Evaluate The Given Integral By Changing To Polar Coordinates R 4x Y Da Homeworklib

Solved Evaluate The Given Integral By Changing To Polar Chegg Com

Solved Evaluate The Given Integral By Changing To Polar Chegg Com

Solved 7 14 Evaluate The Given Integral By Changing To Polar Coordinates Iint R Arctan Y X D A Where R Left X Y 1 Leqslant X 2 Y 2 Leqslant 4 0 Leqslant Y Leqslant X Right

Convert Double Integral Using Polar Coordinates Youtube

Solved Evaluate The Iterated Integral By Converting To Polar Chegg Com

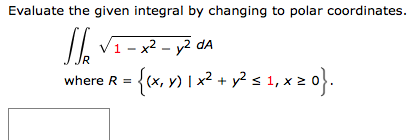
Solved Evaluate The Given Integral By Changing To Polar Chegg Com

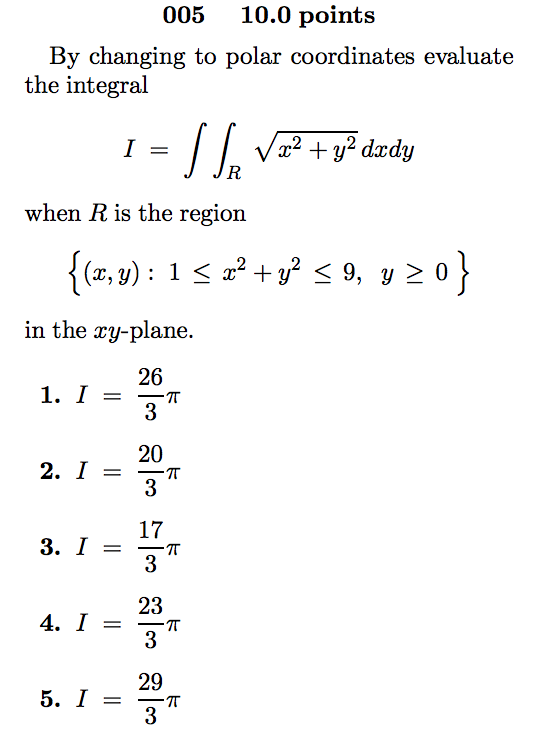
Solved By Changing To Polar Coordinates Evaluate The Chegg Com

Solved By Changing To Polar Coordinates Evaluate The Chegg Com

Solved Evaluate The Given Integral By Changing To Polar Coordinates Begin Array L Iint D E X 2 Y 2 D A Text Where D Text Is The Region Bounded By The Text Semicircle

Solved Evaluate The Given Integral By Changing To Polar Chegg Com

Integration Simple Double Integral In Polar Coordinates Exercise Changing It To Polar Coordinates Mathematics Stack Exchange

Solved Evaluate The Iterated Integral By Converting To Polar Chegg Com

Evaluate The Iterated Integral By Converting To Polar Coordinates 2 0 Sqrt 2x X2 0 6 Sqrt X2 Y2 Dy Dx Studentshare

Solved Evaluate The Iterated Integral By Converting To Polar Chegg Com

Solved Evaluate The Integral By Changing To Polar Chegg Com

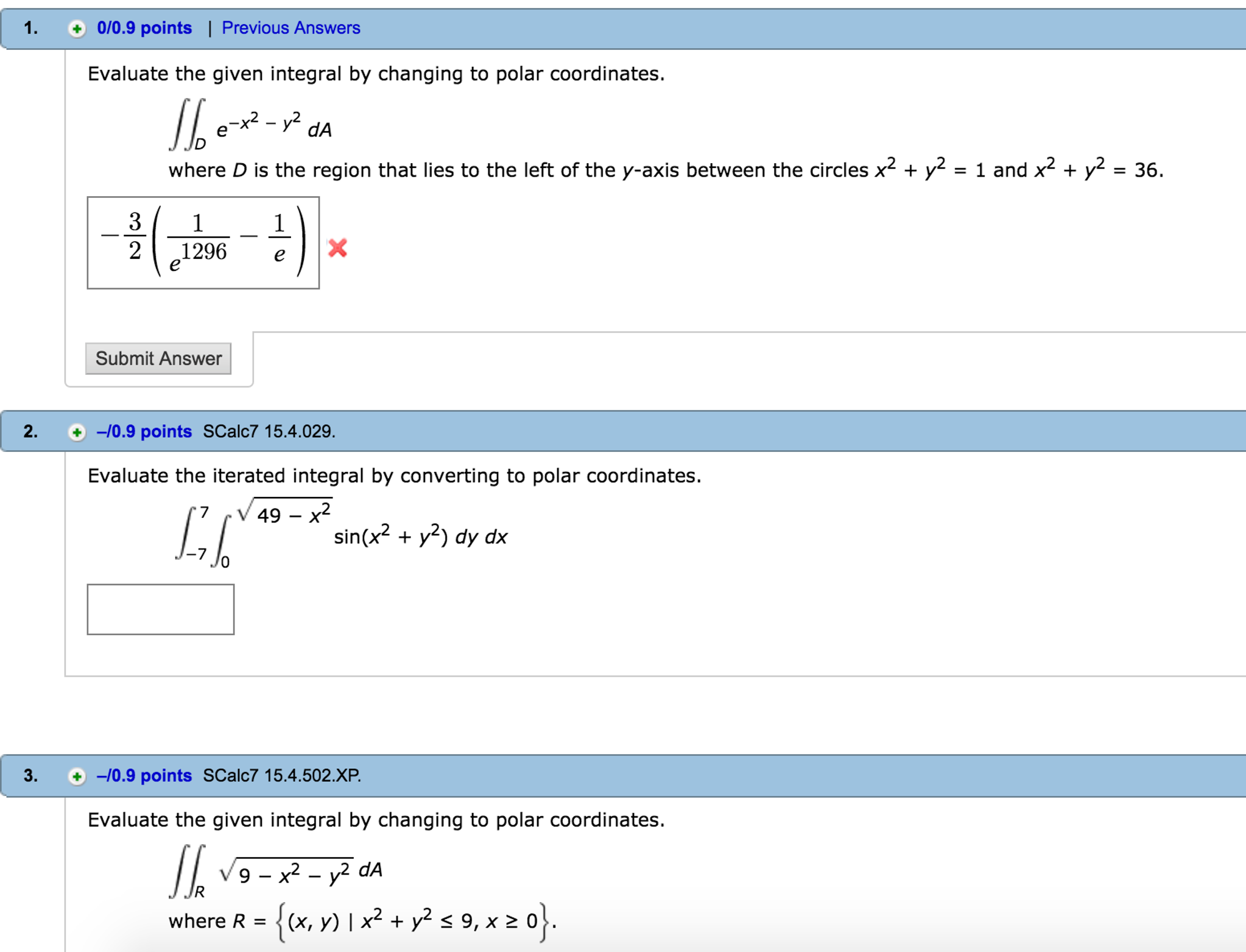
Solved Evaluate The Given Integral By Changing To Polar Chegg Com

Evaluate The Integral Below By Changing To Spherical Coordinates Y2 100 100 10 10 X2 Y Y2 Homeworklib

Solved Evaluate The Given Integral By Changing To Polar Coordinates Begin Array L Iint D E X 2 Y 2 D A Text Where D Text Is The Region Bounded By The Text Semicircle